A simple statement about complex functions
Reflections on Euler's equation
A year or so ago I wrote an article about the search for simplicity in various fields — including poetry, science, philosophy, and religion.
I mentioned as an example the celebrated mathematical statement known as "Euler's equation" or "Euler's identity":
e i π + 1 = 0
It's a statement that is written very simply, but does require effort to understand, unless you are already familiar with the concepts surrounding it.
The effort we take to make sense of the equation may reward us with a better understanding of what sort of simplicity it represents.
Explanation of the symbols
In Euler's equation
- The symbol π represents pi, the ratio between the circumference and diameter of a circle.
- The symbol e represents the base of the natural exponential function (explained below).
- The symbol i represents the square root of minus one.
Euler's Equation and Euler's Formula
The immediate source of Euler's Equation is a more general statement known as Euler's Formula,
e i x = cosine x + i sine x
where "sine" and "cosine" are functions of an angle in radians (or functions of a real number), not functions of an angle in degrees.
Euler's Formula was first published in its current form in 1748 by the Swiss mathematician Leonhard Euler.
* * * * * * * *
A paradox and a jewel?
The nineteenth century American mathematician and philosopher Benjamin Peirce described the Equation as "absolutely paradoxical". Readers of the journal Mathematical Intelligencer in 1990 voted it the "most beautiful theorem in mathematics". The twentieth century physicist Robert Feinman called Euler's Formula "our jewel".
According of Edward Kasner, author of the book Mathematics and the Imagination: "It appeals equally to the mystic, the scientist, the philosopher, the mathematician. For each it has its own meaning."
* * * * * * * *
Why I found it weird and intriguing
It was in Kasner's fascinating book that I first encountered Euler's equation many years ago, when I was still going to school. Kasner presents the equation, without explanation, at the end of a chapter about irrational and imaginary numbers. I found it weird and intriguing, but it was several decades before I looked into it further...
The concepts of pi, e, and i are intriguing in themselves. Pi and e are known technically as irrational numbers, meaning that they cannot be expressed exactly as ratios of whole numbers. It follows that they cannot be expressed exactly as terminating or recurring decimals; although they can be approximated. Pi is approximately 3.14159, and e is approximately 2.71828.
The number i, the square root of minus one, is an imaginary number, as distinct from the real numbers (positive numbers, negative numbers and zero). It cannot be written as a decimal, even approximately.
The real numbers can be situated on a horizontal number line, with zero in the middle, the negatives on the left and the positives on the right. The number i is nowhere on this line. It can however be situated in a two-dimensional space called the complex plane. Each point in the complex plane corresponds to a complex number, of the form a + i b.
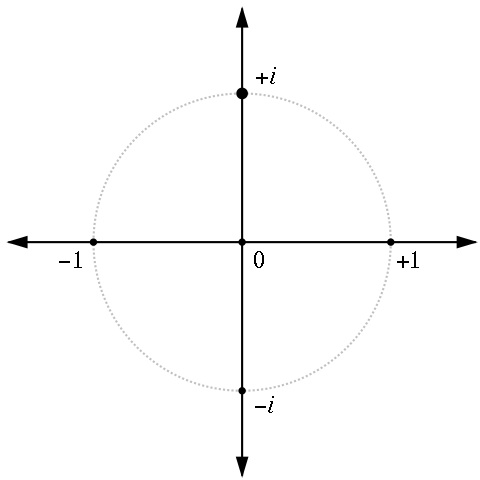
Pi, e, and i are instances of the way the concept of number has gradually been extended. The number zero is another instance of this. The concept of zero as a number emerged in India, where it was denoted by the Sanskrit term śūnya (void). The mathematician Brahmagupta (seventh century CE) was the first to formulate rules for equations containing zero.
When extending mathematics to include more sorts of number, mathematicians have historically tried to extend familiar rules of calculation into the new territory, unless it can be shown that the extension results in logical inconsistencies. (Logical inconsistencies can appear, for instance, if you try to extend the operation of division to include division by zero.)
If we entertain the idea of a number called i, whose square is minus one, then familiar rules of calculation, such as the associative principle, can be used to work out (for instance) that
i 3= i.i.i = i 2.i = -1.i = - i
and
i 4= -1 2= 1
Also that
-4 = (2i) 2
and that in fact every negative number has a square root which is i multiplied by a real number.
An expression like e i π still looks strange though. Taking the everyday definition of expressions like a b or x y, are we being asked to imagine a product of the form
e.e.e...
where the total number of all these e's happens to be pi times i ?? How can that mean anything?
* * * * * * * *
Why it makes sense
There are other definitions of expressions like a b or x y apart from the repeated multiplication definition. For instance, a definition can be based on the relations a b.a c = a b+c and (a b) c = a b.c. Another way of defining these expressions is by beginning with the natural exponential function e x.
The natural exponential function: growth and decay
The natural exponential function e x or exp (x) can be defined in terms of the following two characteristics:
- Its output and its output's rate of change are always equal. In other, more technical words, it is a function whose derivative function is itself.
- When its input x is 0, its output is 1.
Expressed in mathematical symbols:
- exp′ (x) = exp (x), and
- exp (0) = 1
Expressed as a graph, the natural exponential function is a rising curve whose slope (gradient) at any given point is always equal to its height (vertical coordinate) at that point.
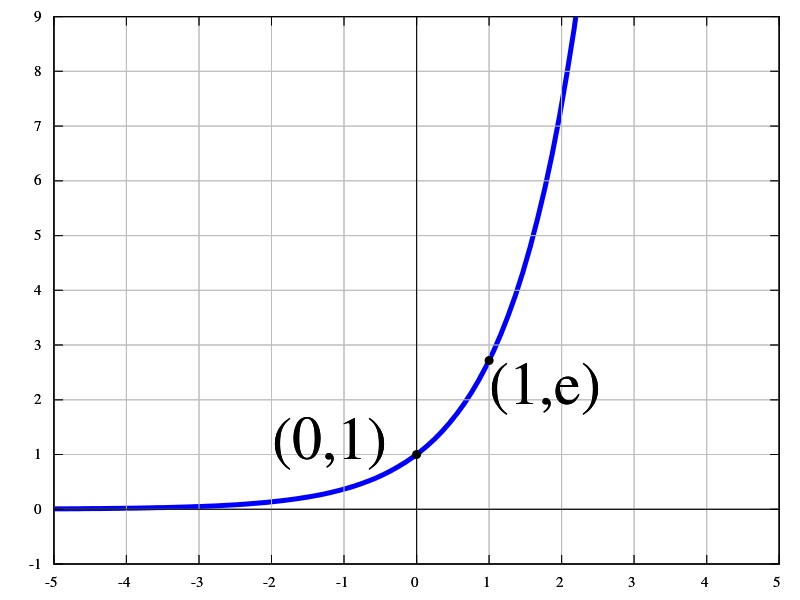
The above definition of e x does not contradict the repeated multiplication definition of exponent. For instance, e 2 is indeed e multiplied by e.
The mathematics of the natural exponential function is relevant to a range of material situations involving growth, from economics (compound interest), to biology (growth of a population of organisms).
Now let's have a look at the function e kx, where x is the input of the function and k is a constant. At what rate does the output now change per change in the input x?
The way the exponential function works is hardly going to change if we represent its input by a different letter. In principle, we could just as well write e y or e z instead of e x. Or we could use two letters. Instead of saying that the rate of change of the output of e x is e x, we could say that the rate of change of the output of e kx is e kx. Note, though, that this is the rate of change per change in kx, and NOT per change in x.
What we wanted to know was the rate of change of e kx per change in x. So the result has to be scaled by a factor of k. Thus...
Where f (x) = e kx, f ′ (x) = k.e kx
(This formula can be used to work out the rates of change for functions such as 2 x or 10 x with the help of the natural logarithm.)
In the case where k equals -1, the function e kx can be written e-x. In this case, the slope of the curve that graphs the function is always negative (downwards), because it is -1 times the height. Whereas the function ex is about growth, the function e-x is about decay. For instance, in nuclear physics it is applicable to the way a radioactive substance diminishes in quantity over time.
Exponential growth gets faster and faster. Exponential decay gets slower and slower.
The wave functions: sine and cosine
The concept of sine, like the concept of zero as a number, comes from India's mathematical literature in Sanskrit, and reached Europe via the Arab world.
The sine function can be defined in terms of a right angle triangle (opposite over hypotenuse) or in terms of a circle (vertical coordinate of a point on a circle of unit radius).
Sine can also be thought of as "acceleration opposite to your current position"(a quote from the website Better Explained, Kalid Azad's intuitive approach to mathematical concepts).
This description works because acceleration is the second derivative of position in relation to time. Velocity is the rate at which position changes, and acceleration is the rate at which velocity changes. It is the rate of change of the rate of change of position.
Sine is the function
- whose second derivative is minus one times the output of the original function;
- which has output zero, when its input is zero; and
- whose output has a rate of change of 1, when the input is zero.
Expressed in mathematical symbols:
- sin″ x = - 1 sin x
- sin 0 = 0
- sin′ 0 = 1
Cosine is closely related to sine. We can think of it as sine's first cousin. It also happens to be the first derivative of sine. The first derivative of cosine is sine times -1.
- cos x = sin′ x
- cos′ x = -1 sin x
Cosine can alternatively be defined without reference to sine, as the function which has the following characteristics
- cos″ x = -1 cos x
- cos 0 = 1
- cos′ 0 = 0
The graph of the sine function is a rising and falling curve called the sine wave, which repeats with a period of 2 π. The graph of cosine looks like the graph of sine, but shifted horizontally.
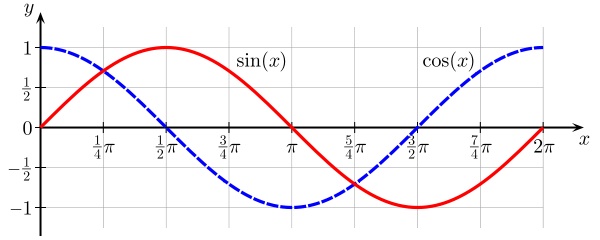
The sine wave is an important concept in the study of oscillating systems, both natural and artificial; for instance, in the physics of sound and in electronics. It is also relevant to the study of waves in water.
Comparing the characteristics of natural exponential function with sine and cosine, such as output and slope when the input is zero, there is clearly stuff in common.
Remember, we defined the exponential as the function
- whose derivative is itself, and
- whose output, when the input is zero, is 1 (same as cosine)
From which it follows that
- its slope, when the input is zero, is 1 (same as sine)
- its second derivative is itself
Viewed this way, sine and cosine start to look like a version of the exponential function which has fissioned into two functions, the second derivatives of which have been transformed by a factor of minus one.
Can the relationship between the exponential function and the sine and cosine functions be captured in a mathematical formula, with the help of the number i?
An exponential function which behaves like sine and cosine
Looking at the second derivative of e kx...
By the same reasoning we used to work out that the first derivative of e kx is k.e kx, we find that the second derivative of e kx is k squared times the output of the original function e kx.
Where f (x) = e kx, f ″ (x) = k 2.e kx
What happens if k is the number i, the square root of minus one?
If g (x) = e ix,
- g′ (x) = i.e ix and
- g″ (x) = i 2 e ix = -1 e ix
So now we have an exponential function whose output times -1 is the second derivative of the function. That means the output's acceleration is opposite to its current position. Just like sine and cosine...
The function "cos + i sine"
If we consider the function cos x + i sin x, sometimes called cis x... Its first derivative works out as the output of the original function multiplied by i.
cis′ x = cos ′ x + i sin ′ x = - 1 sin x + i cos x = i.cis x
The output of cis x, when the input is zero, is the same as for cos x, namely 1. The characteristics of cis x can be summarised as
- cis 0 = 1
- cis′ x = i.cis x
Another characteristic, which follows logically, is
- cis″ x = -1.cis x
Compare g (x) = e ix, whose characteristics are
- g (0) = 1
- g′ (x) = i.g (x)
- g″ (x) = -1.g (x)
So the two functions cis x and e ix have the same output when x equals 0; and the first and second derivatives (rates of change) for the two functions work the same way. This is more than enough to establish that cis x and e ix are actually the same function.
e ix = cis x = cos x + i sin x
The variable in these equations doesn't have to be written "x ". In principle, any letter could be used. In practice, the Greek letters "θ" (theta)" or "φ " (phi)" are frequent alternatives. So the just-mentioned equation is often written
e i φ = cos φ + i sin φ
φ or θ is used, because these symbols are by convention associated with angles. The cis function (and therefore also the exponential function equivalent to it) can be represented on the complex plane by showing its input as an angle rather than a linear measure.
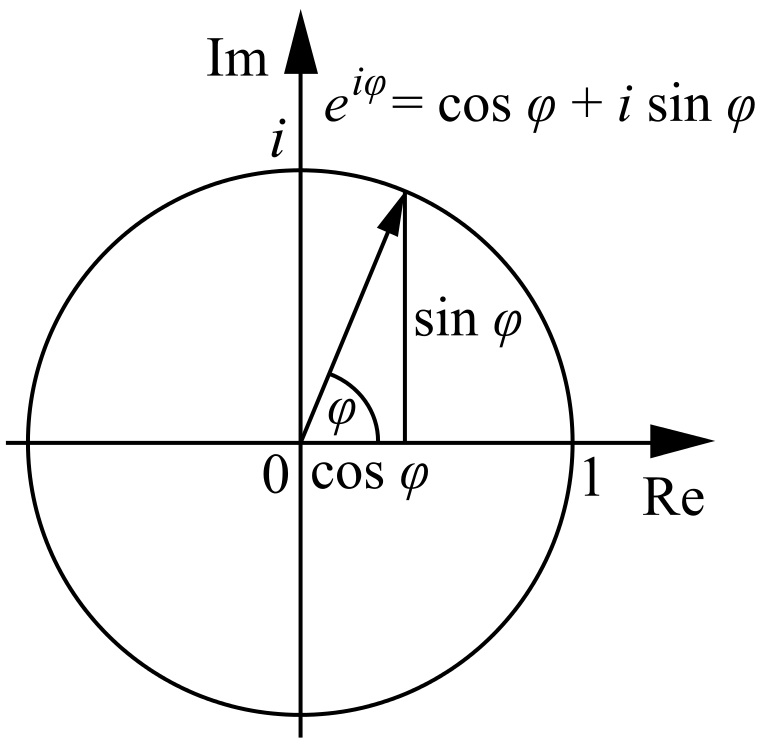
e i φ with input variable φ shown as an angle
Because sine π is 0, and cosine π is -1, it follows that
e i π = -1
Therefore
e i π + 1 = 0
* * * * * * * *
What sort of simplicity does Euler's equation represent?
There is more than one sort of simplicity.
There is the simplicity which rejects complications, and the simplicity which works with complications. The first of these is like a shop with only a few sorts of goods on its shelves. The second is like a shop where a great range of goods are organised and presented so as to make it as easy as possible to find what you want.
The simplicity of Euler's identity is simplicity that works with complication. It is simple but not simplistic. In this respect I consider it a model for the simplicity worth searching for in other fields, as well as in mathematics.
What about...
Natural logarithm and power series (or Taylor series) are two concepts often mentioned in discussions about Euler's equation. While they are interesting and relevant, they are not strictly necessary in order to see why the equation makes sense.
Natural logarithm
Natural logarithm is the inverse function of natural exponential. In other words, it is the natural exponential function with input and output reversed. If it is true that y = e x, then it's also true that x = ln y where ln means "natural logarithm". The natural logarithm corresponds to an area under a section of a hyperbola, and is therefore also called the hyperbolic logarithm. Natural logarithm emerged historically as a concept before the natural exponential function, so e is often explained as "the base of the natural logarithm".
Natural logarithm can be used to convert an exponential function with another base into the natural exponential function. E.g. 10 x is equal to e x.ln10. If follows that the rate of change of the function 10 x is the function's output scaled up by a factor of ln 10. (The natural logarithm of 10 is approximately 2.3026.)
Power series
Power series are a way the exponential, sine and cosine functions can be calculated, or indeed defined:
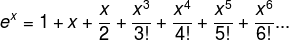
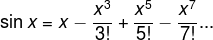
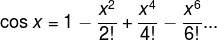
(The exclamation marks in these series denote the factorial operation, that is, 3! means 3×2×1, 4! means 4×3×2×1 etc.)
Comparing these series, we see that the power series for sine and cosine together contain all the terms in the power series for the exponential function, except that the series for sine and cosine have minus signs in some of the places where exponential function's series has a plus sine. By substituting ix for x in the power series of the exponential function, and by multiplying the sine power series by i, we arrive at Euler's formula.
The fact that these power series fit together so neatly may look like a very lucky chance, but is actually a natural consequence of the function characteristics we looked at earlier, namely the output of each function when its input is zero, and the way its output changes as the input changes.
Colin Robinson, June 2015
Text © Colin Robinson 2015
Graphics obtained through Wikimedia Commons. For authorship and licensing information see:
Comments
From Sanjay Dey…
20 July 2015
It's really very interesting. Though I don't know anything about maths, and remembers vaguely the exponential, algorithims etc. but I liked the way you simplified. In Maths there are many theories which is paradoxical in nature.
thanks for sharing.
Namaste.
Sanjay
From Michael McPhee
27 December 2015
A Choilm, a dhearthair
Great to hear from you... I looked around your site to refresh my memory and chanced across your article on Euler's equation - very clearly explained.
Well, I have a natural log equation for you (see below)...
Slan go foill,
Micheal
Send us your comments
Share your thoughts about this article with the rest of us. Email
feedback<colin@weareferment.net>
Or use this form to send your email automatically *...
* This method will work if your browser handles "mailto" links. If we don't acknowledge your on-topic message, feel free to resend it another way!

